¿Arquitectura fractal?

Según Francisco Martínez Cendra, viejo amigo de área fractal, «...aquellas personas que lo manejan lo guardan celosamente como aquellos francmasones de la antiguedad que construyeron las catedrales góticas y se guardaban sus secretos...», refiriéndose al tema de la aplicación de algoritmos fractales a la arquitectura.
Lo cierto es que, si existe información clara sobre el tema, se sabe esconder muy bien. No obstante, aquí van algunos enlaces: The fractal mind in the new architecture, Fractal architecture, Fractal geometry in the late work of F. Lloyd Wright, Fractal modelling of diffusive urban configurations, Fractals in architecture, Fractal geometry in architecture, Fractal geometry in architecture & design, TreeTown, Pavements as embodiments of meaning for a fractal mind, A scientific basis for creating architectural forms, Fractal rhythms as a pathway toward nature oriented architecture.
Percepción
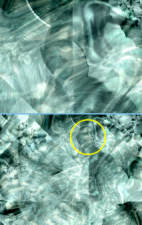

Me han preguntado en algunos mensajes la razón por la cual incluyo una figura humanoide en una de las imágenes de las galerías (alchemy #18). Mi respuesta es que no es así, y de hecho, al observar de cerca la zona en cuestión (imagen superior izquierda), se puede apreciar que es un caprichoso resultado de los filtros, las fórmulas y las mezclas, que demuestra nuestra tendencia natural a buscar caras en cualquier sitio (montañas, nubes, cúmulos de grasa en el cocido, etc.).
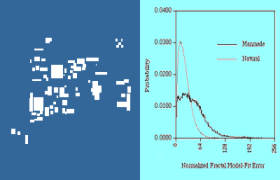
Y puestos a analizar las intrincadas conexiones mentales, me vino a la memoria la "cara de marte", una formación montañosa situada en la región marciana de Cydonia, fotografiada por vez primera en 1976 por la sonda espacial Viking (imagen superior derecha, arriba). Cuando en 1998 volvieron a tomarse fotos de la región con la mejor óptica de la Mars Global Surveyor (imagen superior derecha, abajo), se imponía un verdadero ejercicio de fe para seguir viendo algo parecido a un rostro humano. Sin embargo, el entusiasmo de todos aquellos que no sólo habían identificado esa "esfinge", sino también una pirámide y una ciudad, les ha llevado a seguir analizando los datos disponibles. Entre otros análisis se han aplicado modelos fractales (figuras inferiores) que ofrecen resultados muy diferentes para la cara con respecto a sus alrededores, lo cual dicen es una evidencia de artificialidad.
No voy a entrar en detalles sobre por qué no creo que la "cara de marte" sea artificial pero, para todos aquellos que siguen buscando aplicaciones grotescas de la geometría fractal, esta es otra respuesta.
La dimensión del universo
En los diferentes grupos de noticias relacionados con los fractales, se está discutiendo mucho últimamente sobre el valor de la dimensión del universo. Una opinión, quizá más poética que otra cosa, asegura que es Pi. Realmente se está estudiando el tema a muy alto nivel, en el sentido de averiguar si la distribución de las galaxias es homogénea a diferentes escalas. Y en otra vertiente, también se analiza la estructura fractal de los "agujeros negros". Ciertamente, a los que sepan algo de geometría fractal, no les resulta extraño un espacio de longitud infinita encerrado en otro finito de dimensión superior.
En el artículo dimensiones no desvelamos la verdadera estructura del cosmos, pero aclaramos algunos conceptos sobre el concepto de dimensión.
La versión 20.0 de Fractint
La última versión del programa se puede descargar gratuitamente desde la página de Fractint. Realmente, ya está disponible la revisión 20.01.7, que soluciona pequeños problemas de la 20.0. Lo más espectacular es la nueva pantalla de desarrollo. Mediante esta opción podemos visualizar a la vez una rejilla con docenas de versiones de una misma imagen calculadas a partir de diferentes valores de parámetros.
Otras novedades de alcance son la ampliación del límite en el tamaño de las imágenes (de 2048 píxeles a 32767) y la inclusión de nuevos algoritmos de coloración.
Y por fin Fractint deja de ignorar la tarjeta de sonido. Se incluye una pantalla de configuración de la salida de audio que nos permitirá escuchar el sonido de las órbitas de Lorenz (por ejemplo) con un poquito más de calidad.
Escher y los fractales
Las últimas versiones de Fractint, incluyen un fractal denominado Escher-Julia. Como es lógico, está relacionado con una serie de ilustraciones de M. C. Escher denominadas "Límites Circulares".
En área fractal, existe un artículo dedicado a Escher, que expone información sobre la serie citada, y también sobre otros aspectos de su obra. Como anécdota, se incluye una reproducción de la más larga de sus "metamorfosis" en formato continuo.
Sierpinski en el siglo XII

El mosaico de la foto adorna el suelo de la catedral de Anagni (Italia), construida en el año 1104. Estos "triángulos de Sierpinski" de orden 4 son, probablemente, los fractales más antiguos dibujados por el hombre. Waclaw Sierpinski, quizá sin conocerlos, los dotó de rigor matemático ochocientos años después. Del triángulo de Sierpinski y de otras estructuras de la mismo índole trata nuestro artículo: Koch y Sierpinski.
La curva Dragón
El hecho de que la curva dragón fuera descubierta por un físico de la NASA (J.E. Heighway), no quiere decir que naciera de complicados cálculos de física cuántica. Realmente fue mientras doblaba una tira de papel, en un acto probablemente involuntario. Para revivir en tus propias carnes ese histórico momento, consigue una tira de papel, y dóblala sucesivamente por la mitad. Cuantas más veces consigas doblarla, más complicado será tu dragón.

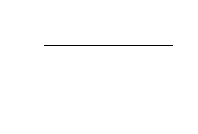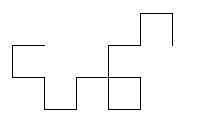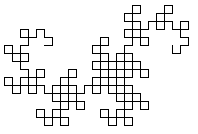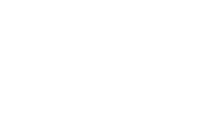
Un método más formal, formulado más tarde por el también físico B.A. Banks, consiste en partir de un segmento y sustituirlo por dos segmentos en ángulo recto. Con cada segmento se va repitiendo la misma operación y así hasta que nos cansemos.
Sonidos fractales
Identificar el término fractal estrictamente con el mundo de la imagen es un error. En primer lugar, ciertas fórmulas están desarrolladas en más de dos (tres, cuatro, etc.) dimensiones, por lo cual podríamos hablar de "esculturas" fractales. Las fórmulas pueden aplicarse a otros campos, entre ellos al del sonido. Por supuesto, del mismo modo que utilizamos técnicas estéticas (color, textura, etc.)con las imágenes, se hace lo mismo con el sonido, de forma que las composiciones resultantes tienen melodía, tempo, armonía, ritmo, y todos los demás elementos musicales, y es la fórmula fractal la que genera en mayor o menor medida todos estos elementos. Puedes oír una composición de ejemplo generada en un par de minutos con uno de los programas gratuitos de música fractal. Hay bastantes direcciones en la red relacionadas con estos temas.
Los "brazos" de Newton
El fractal de Newton nace de una indecisión. Está basado en un algoritmo para calcular por aproximación las raíces complejas de un polinomio. Aplicado a una imagen fractal resulta que cuando la estimación inicial se encuentra a mitad de camino de dos raíces se produce una situación caótica, en la cual el método "no sabe" por cual de ellas decidirse.
Al establecer los parámetros de la fórmula, podemos elegir el número de raíces complejas del polinomio. La versión clásica del newton tiene tres raíces, y el fractal resultante tiene tres "brazos" (fig. 1). Establecer dos raíces carece de interés, aunque se pueden conseguir resultados interesantes aplicando una inversión de radio (fig. 2).




Mención especial merece el caso contrario, o sea, establecer demasiadas raíces. Con mil y pico aparentemente no obtenemos nada. Ello es debido a que los brazos son demasiado delgados, pero obviamente han de estar ahí. Y los descubriremos si hacemos zoom, en la zona central (fig. 3) o incluso a docenas de metros de distancia (fig. 4) de aquélla. El carácter autorrepetitivo del Newton se deja notar.