Maurits Cornelis Escher (Leeuwarden, 1898 - Baarn, 1972) y la palabra imposible quedarán íntimamente ligadas para la posteridad. No hay que analizar con detenimiento su obra para percatarse de que tras sus grabados, técnicamente buenos, se esconden universos más complejos de lo habitual. Su obra está plagada de conceptos geométricos muy interesantes, como la partición regular de la superficie, los cuerpos geométricos complejos, la perspectiva... No es el único artista gráfico que ha explorado estos mundos, pero Escher tenía la virtud de impactar con cada imagen, utilizando para ello su mejor arma, la paciencia, que le llevaba a ensayar una y otra vez diversas posibilidades, hasta dar con la magia. El siguiente comentario, no exento de una exagerada modestia, ilustra su manera de trabajar:
«¡Cómo me gustaría aprender a dibujar mejor! Hacerlo bien requiere tanto esfuerzo y perseverancia... A veces los nervios me llevan al borde del delirio. Sólo es cuestión de batallar sin descanso con una autocrítica constante e implacable. Pienso que crear mis grabados sólo depende de querer realmente hacerlo bien. En su mayor parte algunas cosas como el talento son naderías. Cualquier escolar con unas pequeñas aptitudes podría dibujar mejor que yo. Lo que normalmente falta es el deseo incontenible de expresarse, apretando los dientes con obstinación y diciendo "aunque sé que no puedo hacerlo, sigo queriendo hacerlo"».
Pero, ¿qué tiene que ver Escher con los fractales? Desconozco si alguna vez llegó él a manejar estos términos, aunque bien es cierto que desarrolló con frecuencia estructuras matemáticas complejas y avanzadas mientras continuaba pregonando su desconocimiento total sobre esta materia. Parte de su obra incluye elementos relacionados con el infinito. Según comentó, su aproximación al infinito surgió del modelo de Poincaré, en el cual se puede representar la totalidad de una superficie infinita encerrada en un círculo finito (fig. 5). A partir de aquí desarrolló sus propios modelos, aunque mucho tiempo antes ya había coqueteado con esta idea en dibujos como Evolución II o Más y más pequeño (fig. 6).


Figura 5: El modelo de Poincaré.
Figura 6: Más y más pequeño.
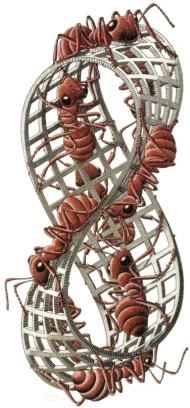
En Más y más pequeño (fig. 6), se puede ver cómo un motivo con forma de lagarto (uno de los favoritos de Escher) es sometido a un proceso de reducción hasta hacerse infinitamente pequeño en el centro de la imagen. Escher grabó, con ayuda de una lupa, lagartos de medio milímetro de longitud. El giro hacia la captura total del infinito se produce con su serie de límites circulares (figs. 7 y 8), donde lo infinitamente pequeño se sitúa en el borde de un círculo, como en el modelo de Poincaré. Otra variante se puede observar en Serpientes (fig. 9), donde los anillos que componen la imagen son infinitamente pequeños tanto en el centro como en el borde.


Figura 7: Límite circular III.
Figura 8: Límite circular IV.
Nos podemos encontrar con fractales que tienen exactamente esa misma estructura (fig. 10). Pese a que los fractales no son invención de nadie, sino que simplemente están ahí esperando a que alguien dé con su fórmula, no me puedo resistir a hablar de fractales "Escherianos", en honor de quien los sacó a luz sin necesidad de fórmulas.


Figura 9: Serpientes.
Figura 10: Un fractal "escheriano".
Figura 1: Boven en onder, litografía, 1947.
Figura 2: Waterval, litografía, 1961.
Figura 3: Band van Möbius II, xilografía, 1963.
Figura 4: Metamorphose, xilografía, 1939-40 y 1967-68.
Figura 6: Kleiner en kleiner, grabado en madera, 1956.
Figura 7: Cirkkellimiet III, xilografía, 1959.
Figura 8: Cirkkellimiet IV, xilografía, 1960.
Figura 9: Slangen, grabado en madera, 1969.
Motivo de fondo: Ensayo para Zwanen, 1956.
Más información sobre la obra de M.C. Escher dentro de la página de Vicent Castellar.