| área fractal | dimensiones |

¿Qué es dimensión?

Bonita pregunta. Lástima que su respuesta no sea única. Una primera definición de dimensión se refiere al número de valores reales que necesitamos para describir cualquier punto en un espacio. Un espacio es un conjunto de puntos, pero no debemos restringir la noción de punto y espacio. Quizá nos sintamos más cómodos manejando conceptos como elemento y conjunto. Así, los libros son puntos en el espacio de la producción editorial, las personas son puntos en el espacio de la población mundial, y cualquier pentágono es un punto del espacio de los polígonos de cinco lados. Según la definición de dimensión que estamos manejando, una línea cualquiera es unidimensional, ya que nos basta un número real para identificar cualquier punto. La línea no tiene por qué ser recta: nos basta un único valor (normalmente el punto kilométrico) para situarnos en una carretera, por muy intrincada que sea. Hasta aquí, todo marcha bien, pero siguiendo el mismo razonamiento, cualquier conjunto finito de puntos también es unidimensional. Hay una diferencia abismal entre un espacio compuesto por diez puntos aislados (es un ejemplo) y el de una línea, formada a la sazón por infinitos puntos, pero la medida de su dimensión no refleja en absoluto esa diferencia.

Otra definición de dimensión se refiere al grado de libertad de movimiento en el espacio. Entenderemos esta libertad como el número de direcciones ortogonales diferentes que podamos tomar. En el espacio que conocemos contamos con tres direcciones: izquierda-derecha, atrás-delante y arriba-abajo. Por ello, decimos que es tridimensional. Podemos definir otros espacios: un tren se mueve en un espacio unidimensional (a no ser que descarrile), un barco en un espacio bidimensional (salvo que naufrague) y un avión en un espacio tridimensional (siempre que haya despegado del aeropuerto). Siguiendo esta segunda definición, el espacio de diez puntos mencionado anteriormente es "cerodimensional". Desde un punto cualquiera es imposible moverse en ninguna dirección, ya que no hay nada entre ese y los demás puntos que componen el espacio.

Todo parece indicar que hemos llegado a una definición más satisfactoria, pero la situación no persiste si analizamos espacios algo más caprichosos. El espacio formado por dos segmentos que se cruzan (figura 2a) sería unidimensional de no ser por el punto de intersección, donde se pueden tomar dos direcciones. Otro espacio (figura 2b) formado por un punto y una superficie, es bidimensional, excepto por el punto, de dimensión 0. Estos diferentes valores se denominan dimensiones locales, y, como vemos, varían dentro de un mismo espacio cuando éste no es homogéneo. Pero aun así, el espacio ha de tener una dimensión global. ¿Cuál escogemos? Si optamos por la mayor, nuestro primer ejemplo, el de los segmentos cruzados, tendría dimensión dos, algo que no es muy sensato. Pero si elegimos la menor, el segundo ejemplo tendría dimensión 0, afirmación muy difícil de digerir.

Cuestiones topológicas

La variante topológica de dimensión sí define pautas fijas para establecer la dimensión global de un espacio a partir de sus diferentes valores locales. En concreto, es el valor máximo. Pero su definición es totalmente diferente a las relacionadas anteriormente.

Para calcular la dimensión local deberemos encontrar un objeto, de dimensión lo más pequeña posible, que nos permita separar una parte del espacio del resto. La dimensión se calcula entonces, simplemente, sumando uno a la de dicho objeto. Así, por ejemplo, nos basta un punto (dimensión 0) para separar dos partes de una línea, por lo cual tiene dimensión 1 (0+1). Para que todo sea perfecto, la dimensión de un espacio vacío se define como -1. De esta forma podremos calcular la dimensión de un conjunto finito de puntos: no nos hace falta nada para separar una parte del resto, luego nos basta el conjunto vacío, y por tanto su dimensión es 0 (-1+1).

Tomando los dos ejemplos del apartado anterior, todo indica que ahora sí obtenemos resultados coherentes. Un punto nos permite romper el espacio en forma de cruz en cualquier lugar, incluyendo la intersección. Es, por tanto, unidimensional. En el segundo ejemplo, tenemos dos valores de dimensión local: 0 y 2. Y el máximo es 2.

Una propiedad interesante en topología es la conservación del valor de la dimensión cuando se realiza una transformación homotópica. Expresado de otra manera: si deformamos un objeto, sin romperlo, perforarlo o soldarlo, conservará su dimensión. La figura 3 es un ejemplo de tal proceso. Pero se da un hecho curioso: si continuamos con una serie infinita de transformaciones siguiendo el mismo patrón (figura 4), resulta que obtenemos una curva que pasa por todos los puntos de una superficie. Si una curva contiene todos los puntos de una superficie, ¿qué la diferencia de ésta? ¿No sería más lógico decir que su dimensión es la misma que la de la superficie?. Más aún: si iterásemos el patrón de la figura 5, la curva resultante tocaría todos los puntos de un cuerpo tridimensional.

Estamos ante dos variaciones de la curva de Hilbert, enunciada a finales del siglo pasado. Estas curvas, debido a su patológico comportamiento, recibieron el nombre de monstruos. Algunos matemáticos pretendieron domarlos indicando que esta clase de transformaciones son "uno a uno", pero no son continuas, por lo cual no son homotopías. De ahí el incremento de dimensión. Desconozco si alguien entendió alguna vez por qué no son continuas... Ciertamente, ni este monstruo, ni ningún otro que se sepa, se ha comido a nadie. Simplemente obligó a buscar otros conceptos de dimensión. Hoy en día podemos encontrarnos con docenas de definiciones diferentes, la mayoría de las cuales son significativamente más complicadas que las anteriores.

El "Efecto Mandelbrot" y la dimensión fractal

¿Cómo podríamos medir la curva de la figura 6a? La idea de medir cada uno de los segmentos de la figura 6b y sumar los resultados parece buena, pero es posible que los detalles que hemos omitido (figura 6c) nos hayan llevado a cometer un error demasiado grande. Esta es la base del artículo «¿Cuánto mide la costa de Gran Bretaña?», publicado por Benoit Mandelbrot. Si hay una imposibilidad manifiesta de realizar una medición exacta, siempre podemos recurrir a un estudio progresivo de la curva, tal y como se muestra en la figura 6d. Se trata de cubrir la curva con el número mínimo de cuadros, cada vez más pequeños.

Vamos a aplicar este método con algo parecido al fractal de Mandelbrot (figura 7). Llamamos h al tamaño de cada uno de los cuadrados, y N(h) al número de los cuadrados que cubren la curva en cada caso. Como el incremento es exponencial, calcularemos logaritmos de cada valor para representarlos:

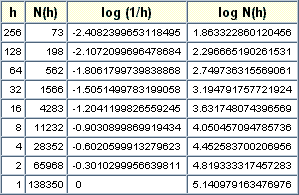
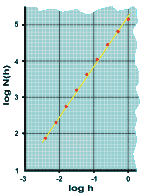
Este método nos permite obtener una aproximación de la dimensión fractal de cualquier objeto, también conocida como dimensión Hausdorff-Besicovitch, cuya fórmula es
D = Lim (log N(h) / log (1/h)),  h ··> 0
y que coincide con la pendiente de la recta del gráfico construido. Hemos obtenido D = 1.38, un valor superior al de su dimensión topológica. Debido a este "pequeño" detalle, la curva es fractal. Por cierto, la verdadera dimensión de la curva de Mandelbrot, calculada por M. Shishikura, es exactamente 2.

Un caso especial es el de las curvas con autosemejanza perfecta (figura 8). Para éstas, la fórmula de dimensión fractal queda reducida a
D = log N(h) / log (1/h)
puesto que la relación es constante. Esto nos permite calcularla fijándonos únicamente en su patrón de semejanza.

Metáforas dimensionales

La existencia de una cuarta dimensión topológica, se ha debatido durante años. Incluso se ha definido alguna figura tetradimensional, como el hipercubo o tesseract. De la misma manera que un cuadrado unitario, desplazado una unidad en dirección perpendicular, forma un cubo, si desplazásemos un cubo una unidad en una dirección perpendicular a las tres que conocemos, formaría un tesseract. Para entenderlo podríamos pensar cómo sería un universo bidimensional inmerso en el nuestro.

Echando mano a este tipo de metáforas se han escrito artículos, novelas y guiones cinematográficos, pero yo me quedo con el episodio 134 de los Simpsons, en el que Homer, huyendo de sus cuñadas, abandona su existencia bidimensional penetrando en un universo de tres dimensiones.

Figura 1: La noción "popular" de dimensión no es todo lo correcta que cabría esperar. A menudo se habla de estructuras bidimensionales o tridimensionales equivocadamente. Por ejemplo, una figura formada por las aristas de un cubo (izquierda) es unidimensional. Si está formada por sus caras (derecha) es bidimensional. Sólo si incluye el interior es tridimensional. La confusión reside en que los tres objetos anteriores únicamente pueden visualizarse en un espacio euclídeo de tres dimensiones. Otro ejemplo: la recta 3w=2x=y=4z es unidimensional, pero cualquier intento de dibujarla es ridículo, porque sólo se podría en un espacio de cuatro dimensiones. ¿Alguien vive en algún sitio así..?

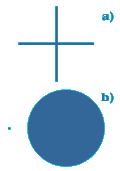
Figura 2

Figura 3

Figura 4

Figura 5

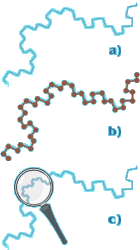
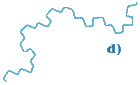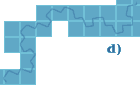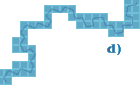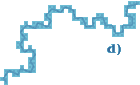
Figura 6

Figura 7

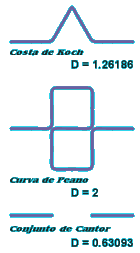
Figura 8

Figura 9