| área fractal | koch & sierpinski |
Curvas de Koch y Sierpinski
En 1.904 Niels Helge von Koch (1870-1924) define la curva que lleva su nombre. Se forma (fig. 1) partiendo de un segmento el cual es dividido en tres partes iguales. La parte central se sustituye por dos segmentos del mismo tamaño que el eliminado. Sucesivamente se repite el mismo proceso por cada segmento formado. La longitud de esta curva evoluciona de acuerdo a la siguiente sucesión:
1, 4/3, 16/9, 64/27, 256/81... , L=(4/3)^k .
Dado que la sucesión anteriormente indicada no converge hacia ningún valor, estamos ante una curva de longitud infinita. Y no sólo eso, sino que cualquier intervalo entre dos puntos también cumple esta propiedad. Otra característica de todos sus puntos es que son no derivables, es decir, es imposible trazar una tangente en ninguno de sus puntos.
Alrededor de 1915, Waclaw Sierpinski (1862-1969) concibió su archiconocido fractal (fig. 2). Partiendo de un triángulo (no tiene por qué ser equilátero) dibujamos otro uniendo los puntos medios de sus lados. La figura resultante contiene cuatro triángulos semejantes al anterior, pero sólo tres comparten su orientación. Ese cuarto triángulo no pertenece a la curva, y este detalle desencadena propiedades sorprendentes. En la siguiente iteración repetimos el mismo esquema con los tres triángulos aludidos, y así sucesivamente. No es difícil observar que el área definida va decreciendo con arreglo a la sucesión (en el caso de un triángulo equilátero de área 1):
1, 3/4, 9/16, 27/64, 81/256... , A=(3/4)^k .
Por tanto, el área total del triángulo de Sierpinski es nula (obviamente tras infinitas iteraciones). Por otra parte, el perímetro de todos los triángulos generados sí es infinito. Siendo 1 la longitud del lado del primer triángulo, el perímetro total crece así:
3, 9/2, 27/4, 81/8, 243/16... , P = 3×(3^k)/(2^k) .
Variaciones
La variación más conocida de la curva de Koch es el "copo de nieve" (fig. 3), que no es más que tres curvas que inicialmente forman un triángulo equilátero. Como no es mi propósito llenar esta página de números, y ya he incluido demasiados, simplemente indico que su perímetro es, por supuesto, infinito, pero que su área tiende a 8/5 del valor del área inicial.
Para "rizar el rizo", nada como las estructuras "tridimensionales". Vamos a utilizar el tetraedro, poliedro regular de cuatro caras, todas ellas triángulos equiláteros. Hay una serie de propiedades de los tres poliedros "menores" (octaedro, cubo o hexaedro y tetraedro) no demasiado conocidas. Por ejemplo, sólo el cubo puede llenar totalmente el espacio por repetición, pero sin embargo la combinación apropiada de tetraedros y octaedros también. Pese a que pueda parecer que el cubo y el tetraedro no se llevan nada bien, resulta que si trazamos las dos diagonales de cada cara de un cubo (fig. 4) obtenemos dos tetraedros. Además, la intersección de esos dos tetraedros (fig. 5) resulta ser un octaedro (dado que el octaedro también puede generar un cubo, esta secuencia puede hacerse infinita, y cada nuevo cuerpo generado es tres veces menor al anterior del mismo tipo). Estas propiedades quedarán patentes en las dos estructuras que propongo a continuación.
El "tetraedro de Sierpinski" (fig. 6) funciona igual que el triángulo, pero al trazar cuatro tetraedros en cada uno de los vértices del original, lo que generamos en la parte central es un octaedro. Como, al contrario de lo que ocurre con la curva de Koch, el Sierpinski alberga todo su interés en su interior, he optado por una estructura transparente.
El "tetraedro de Koch" (fig. 7) se forma "recortando" un triángulo invertido en cada lado (de manera idéntica al Sierpinski) y sustituyéndolo por un tetraedro. En la práctica, esto es lo mismo que intersecar en cada tetraedro otro de iguales medidas para formar una estrella. De forma similar al caso del Copo de nieve, el área superficial tiende a infinito. Lo más espectacular: El volumen tiende al de un hexaedro cuyas diagonales laterales miden lo mismo que la arista del tetraedro original, igual que en el caso comentado respecto al modelo de la figura 4. De hecho, tras unas pocas iteraciones, el tetraedro se convierte en un cubo ante nuestra sorpresa.
Figura 1

Figura 2

Figura 3
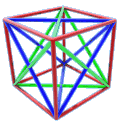
Figura 4
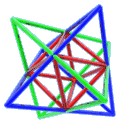
Figura 5
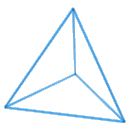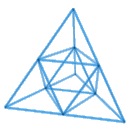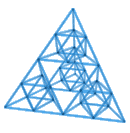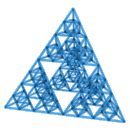
Figura 6

Figura 7
· área fractal · sysifus, 11 de marzo de 2000. ·