| área fractal | caos |
Las mariposas influyentes y el nuevo traje del emperador
Vivimos en el caos. Realmente lo asumimos inconscientemente, mientras tratamos de ordenar, catalogar y adivinar el entorno, sus elementos y acontecimientos. Es paradójico que una maquinaria tan inmensa como un sistema solar tenga un comportamiento más predecible que una hoja de papel que se cae de nuestra mesa. De ahí el término cosmos, que significa orden. Pero, cuán desordenado resulta el orden cuando se observa con la precisión adecuada. Mientras tanto, llamamos caos a todo aquello que no somos capaces de sistematizar. Por eso la palabra en cuestión aparece frecuentemente ligada a fenómenos tan "incontrolables" como el tráfico de una gran ciudad o el funcionamiento de ciertas instituciones públicas.
Se suele relacionar caos con aleatoriedad, una comparación que es fruto de la imposibilidad histórica de manejar ciertos sistemas, pero el concepto mismo de aleatoriedad contiene una trampa casi metafísica: no estamos ante un término objetivo. La trayectoria de una mosca dentro de nuestra habitación nos puede parecer aleatoria, pero a buen seguro que para la mosca no lo es. Y no sólo eso: no podemos crear algo totalmente aleatorio, aunque queda por demostrar si se trata de una imposibilidad trascendental o simplemente práctica. El problema está en saber si realmente Dios jugaba a los dados o seguía unas normas, pregunta formulada por Einstein hace algún tiempo. El tema de la posible ludopatía del creador del mundo o, dicho en otras palabras, la existencia de un elemento de azar en la estructura del universo, entra de lleno en la cuestión del caos.
Todos hemos oído hablar alguna vez del efecto mariposa, que viene a decir que el batir de las alas de una mariposa situada en Indochina puede provocar un tornado en el golfo de México. No deja de ser una metáfora, pero alude a la naturaleza de la atmósfera, uno de los sistemas caóticos más estudiados a lo largo de la historia. No es casualidad que Edward Lorentz, uno de los padres de la teoría del caos, fuera meteorólogo.
Dentro de un sistema caótico, una pequeña variación en cualquiera de sus elementos puede provocar una desviación importante de los resultados. En el cuento "El nuevo traje del emperador" de Hans Christian Andersen, el desenlace final de la historia se produce por la intervención de un niño, que representaba, tanto cuantitativa como cualitativamente, una diminuta parte de la sociedad. Si ese niño no hubiera hablado (los niños, por regla general, están más guapos con la boca cerrada), la población hubiera terminado paranoica y el emperador habría muerto de pulmonía al invierno siguiente. No es difícil encontrar ejemplos reales en los que un suceso, nimio a priori, desencadena una serie importante de acontecimientos.
De leyes y demonios
Existen dos tipos de sistemas: estáticos y dinámicos. En los primeros, todos sus elementos permanecen estables por los siglos de los siglos, y parece ser que sólo existen en los libros de texto. En los sistemas dinámicos, por el contrario, hay parámetros que evolucionan con el transcurrir del tiempo, y los científicos han tratado de establecer fórmulas para predecir su comportamiento, con mayor o menor éxito. El universo es un gigantesco sistema dinámico gobernado aparentemente por unas pocas leyes sencillas, enunciadas por Isaac Newton hace poco más de tres siglos. Ecuaciones ulteriores, como las de la relatividad general, simplemente advierten que en ciertas circunstancias, nada cotidianas, la mecánica clásica no es todo lo universal que Sir Isaac había pensado. Correcciones relativistas aparte, estas leyes determinan que, bajo circunstancias idénticas, obtendremos también resultados iguales, y si las circunstancias varían ligeramente, el resultado cambiará proporcionalmente. El lanzamiento parabólico de un proyectil, de gran popularidad entre los autores de libros para bachillerato, es buena prueba de ello.
Pero tampoco hay que buscar demasiado para encontrar problemas irresolubles. Colocar un huevo en equilibrio sobre su polo estrecho, por ejemplo. Este experimento, solventado por Cristóbal Colón en 1493, ha sido imposible para el resto de los mortales. Las malas lenguas dicen que el navegante hizo trampa, pero quién sabe... En cualquier caso, tan difícil es poner un huevo de pie como adivinar hacia dónde caerá. Depende de multitud de variables: la propia naturaleza del huevo, la superficie, el aire, e incluso esa microscópica mota de polvo que puede resultar determinante. Calcular previamente la trayectoria de nuestro huevo requeriría el conocimiento preciso de todos esos datos y de todas las fuerzas a las que está sometido en el momento inicial de equilibrio, lo cual es imposible, salvo para el Demonio de Laplace. Este personaje tiene un conocimiento pleno de todas las fuerzas de la naturaleza y de la situación de todos los elementos, y por tanto nada es incierto para él, ni el pasado ni el futuro. Si el Demonio de Laplace fuese infalible, el caos sería para él un término sin sentido. Pero, tal y como vamos a comprobar, sólo un error entre miles de millones de aciertos, por diminuto que fuese, dotaría a sus predicciones de la misma fiabilidad que la de un horóscopo telefónico.
La influencia sensible
No debe entristecernos el hecho de no poder acceder a toda la información conocida por el personaje creado por Pierre Simon de Laplace. Gracias a nuestra fenomenal ignorancia, actividades tan edificantes como una partida de billar tienen un desenlace incierto, aun cuando los jugadores sean mejores que "Felson el rápido". Esta paradójica comunión entre lo impredecible y lo determinista nos libera de lo que, de otra forma, sería un aburrimiento cósmico. Ya adelantábamos antes el comportamiento de los sistemas dinámicos "amables", en los cuales existe una relación clara entre circunstancias y resultados. Como si de un lobo con piel de cordero se tratase, el caos se esconde en sistemas con esta inocente apariencia.
Los datos de la tabla en la figura 1 muestran las primeras iteraciones de una fórmula bien conocida por los biólogos. Se trata de la curva logística, utilizada para estudiar la evolución de poblaciones en ecología. Las tres columnas corresponden a tres valores iniciales tan próximos como 0.199, 0.19999 y 0.1999999. Después de unas pocas iteraciones, los resultados oscilan entre 0 y 1 sin ninguna correlación. Se podría argumentar que los valores elegidos son muy diferentes, pero lo cierto es que, con valores iniciales infinitamente más próximos, obtendríamos el mismo galimatías. Bajo esta tesitura, cualquier pequeño redondeo o aproximación nos llevará irremisiblemente a un error de magnitud desconocida, y la dramática pregunta es: ¿jugamos alguna vez con datos exactos?. Esta terrible influencia de las condiciones iniciales, que nos conduce a una desazonadora incertidumbre, es la auténtica definición de caos.
La impredecibilidad, en contra de lo que pueda pensarse en un primer momento, puede representarse gráficamente. La figura 2 muestra el diagrama de bifurcación correspondiente a la función logística. De los infinitos caminos contemplados en el gráfico, sólo uno es el correcto. Pero mientras tanto, y en la porción de curva existente entre dos bifurcaciones, reina el más absoluto de los determinismos. No deja de ser un agrio consuelo.
Atractores extraños
Siguiendo con nuestro peculiar estudio de los sistemas dinámicos, debemos apuntar que los hay de dos clases: conservativos y disipativos. A efectos prácticos, un sistema conservativo puro es tan improbable como un sistema estático. Los sistemas disipativos están expuestos a la progresiva variación de energía útil y, debido a ello, su evolución queda ligada a una estructura denominada atractor, que puede ser tan complejo como podamos imaginarnos. El atractor es la región del espacio hacia la cual convergen las trayectorias posibles dentro de un sistema. Un péndulo simple es el caso más sencillo. Cualquiera que sea el impulso inicial recibido, el péndulo tiende a estabilizarse siempre en el mismo punto. Complicándolo un poco, si el péndulo contase con una fuente de energía que le proporcionase un movimiento constante, describiría una órbita elíptica. Cualquier intento externo de apartarlo de esa trayectoria es atenuado después de un lapso de tiempo determinado, para volver tarde o temprano a esa órbita. Este tipo de atractor recibe el nombre de ciclo límite.
Estos dos modelos no encajan en un sistema caótico. La sensibilidad a las condiciones iniciales provoca que la estructura del atractor esté formada por una trayectoria que diverge y converge de forma inescrutable. Pero además debe cumplir otra condición: no puede cortarse a sí misma, ya que, si así fuese, habría dos curvas diferentes a partir de ese punto de corte, lo cual significaría dos realidades simultáneas y diferentes. Una curva de estas características no puede estar contenida en un plano, y por supuesto su dimensión es fraccionaria. Este es el punto en común entre el caos y la condición fractal. Los atractores caóticos, como el de Lorentz (figura 3), son difíciles de visualizar y representar. Debido a ello, se denominan atractores extraños, aunque ese adjetivo se quede corto.
Caos en el caos
La realidad se nos presenta, con estos postulados, transparente y opaca al mismo tiempo, y esto puede traer interpretaciones equivocadas y pseudocientíficas. El caos es un hecho, pero también es una circunstancia extrema. Un ejemplo bastante aclaratorio es el de las órbitas planetarias, que si bien tienen una ínfima componente caótica, están infinitamente más cerca de la estabilidad de un ciclo límite que del desvarío incongruente de un atractor extraño. Consciente de que la realidad está plagada de elementos semejantes, Steve Wolfram ha definido un estado entre el comportamiento ordenado y el caos, denominado "límite del caos". Quizá deambulamos constantemente por esa zona gris, más cerca del caos que del orden, mientras nos convencemos de que jamás alcanzaremos la posición del demonio de Laplace.
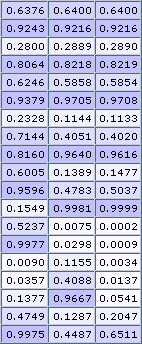
Figura 1

Figura 2

Figura 3
· área fractal · sysifus, 14 de julio de 2000. ·